Bisra effects on the Flat Hot Strip Rolling Mills and Gaugemeter AGC Strip Thickness Correction
Kemal ERKUT
Elektrik Kontrol & Otomasyon Müh., kemalerkut@gmail.com
ÖZET
4HI hadde yapısı içerisinde haddeleme esnasında ezme kuvvetine karşı malzeme tepki davranışlarının matematiksel tanımlamaları, hadde ezme kuvveti etkisine karşılık hadde sıçramasının çıkış kalınlığına etkileri ve şerit malzeme kalınlık düzeltme fonksiyon algoritmaları konu edilmiştir. Kalınlık kontrolü algoritmaları temel esasları özet olarak anlatılmaktadır.
ABSTRACT
In this article, the horizontal rolling forces, mill stretch of stand housing, roll chocks and housing of rolling stand constitution, roll gap setting calculation effects are explained. The 4HI rolling mill stand is analysed and methods are described to improve its rolling performance.
The mill stretch compensation and other disturbances during the rolling process are compensated to accomplish fine strip thickness control. Influence of rolled metal dimensions, mass and speed of rolled metal before metal-in on dynamic forces of work rolls chocks horizontal impacts explained. AGC automatic gauge control menu main functions are subjected below article.
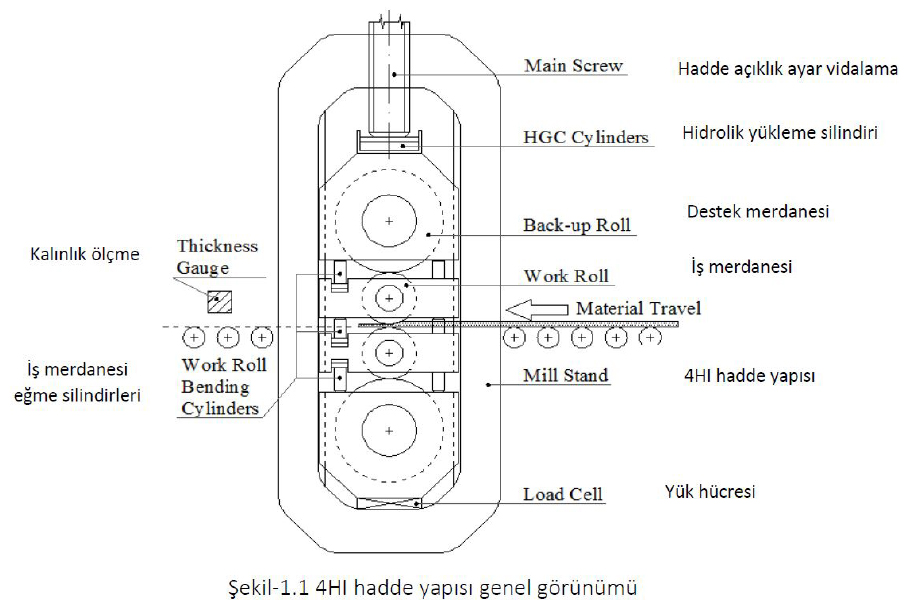
I. Haddelerde Sıçrama Etkisi ve Mill Modulus Tanımlaması
Hadde dizini üzerine haddeleme ezme yükü uygulandığında, 4 HI hadde (mill stand) yapısı bütün olarak elastik deformasyon etkisi gösterecektir. Buna hadde sıçrama etkisi-mill stretch effect- denilir.
Haddelemede iki temel modulus parametresi kullanılır. Bunlar; mill modulus (veya elastik modulus) ve diğeri de plastik modulus olarak adlandırılır.
Mill modulus; haddenin (4 HI mill stand housing) çelik yapısı içerisinde merdaneler dizini, merdane yatakları, mekanik vidalama ve hidrolik yükleme silindirleri yapısı ile birlikte komple ezme kuvvetine karşı tepkime davranışı karakteristiğidir. Bu davranış eğrisi “mill spring curve” hadde sıçraması olarak tanımlanır. Plastik modulus; haddelenen malzemenin merdaneler arasında ezme kuvvetine karşılık verdiği ters tepkime kuvveti ve davranışı karakteristiğidir. Bu davranış eğrisi “material curve” metal tepkimesi olarak adlandırılır.
Haddenin bu sıçrama miktarı, boşta set edilecek hadde açıklığı S0 değerine düzeltme etkisi olarak katılmadığı takdirde, hadde çıkışında talep edilen malzeme kalınlığı farklı sapmalarda olacaktır.
Hadde sıçrama kuvveti ve dolayısı ile sıçrama açıklık değeri (mill stretch curve values) haddelerin ilk devreye alınması aşamasında çıkarılır. Buna “mill modulus eğrisi” denilir.
Hadde sıçrama kuvveti (mill stretch force), haddede malzeme yokken ve belirlenmiş bir hızda merdaneler döndürülürken merdanelere dikey uygulanan kuvvet olup hadde yapısında yerleşik olan iki adet yük hücresi (operatör taraf ve tahrik taraf yük hücreleri) üzerinden ölçülerek veya her iki taraf hidrolik yük silindirleri devresinde var olan basınç transdüserleri üzerinden hesaplanarak kayıt altına alınır. Toplanan bu veriler ile hadde sıçrama eğrisi (mill stretch curve) çıkartılır. Bu eğri, sıçrama ezme kuvveti “mill stretch force” (kN) ve sıçrama açıklık değeri “mill stretch value” (mm) eksenli olup hadde ezme kuvveti yüküne göre non-lineer bir yükseliş gösterir.
Haddenin kalınlık çalışma aralıkları toplam ezme kuvvetine bağlı olmakla birlikte, hadde-mill stand- yapısının elastik deformasyonu ile direkt ilişkilidir. Sıçrama miktarı ezme kuvvetine bağlı olarak birkaç milimetreye kadar ulaşabilir.
Çelik şerit haddelerinde hedeflenen kalınlık sapması toleransı +/- 0,1 mm’den +/-0,4 mm mertebelerine kadar olacağı düşünüldüğünde, kararlı bir ölçümlenmiş hadde sıçrama etkisi kompanzasyonunun önemi anlaşılır. Genellikle şerit haddelerde mill modulus ve sıçrama etkisi eğrisi sabit kabul edilir. Ancak zaman içerisinde haddenin yaşlanmasına bağlı olarak bu eğrinin zaman zaman tekrar çıkarılması ve hadde kalibrasyonunun buna uygun yapılması önerilir.
II. Şerit Haddelemede BISRA Eşitliği ve Boşta Hadde Açıklık Hesaplaması
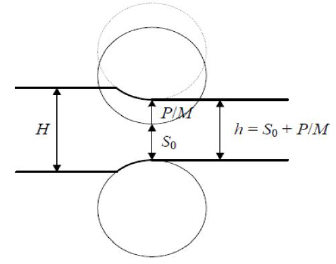
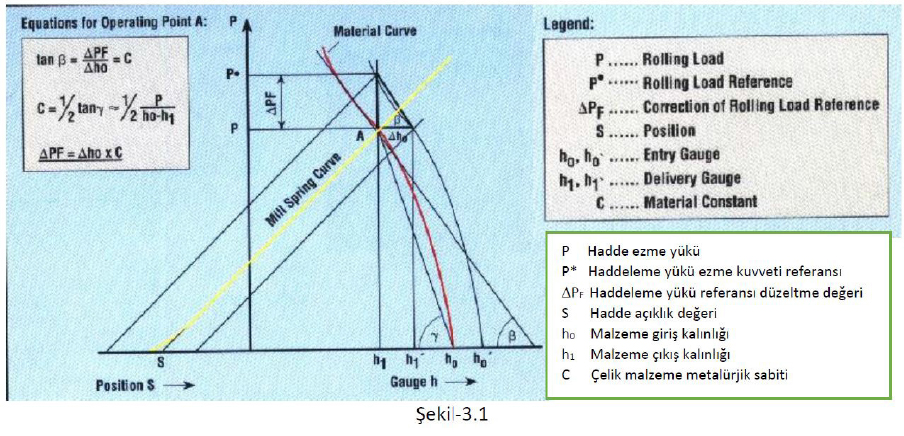
4HI mill stand hadde yapısında haddeleme ezme kuvveti F0, boşta set edilen hadde açıklığı G0, giriş malzeme kalınlığı S0, ve çıkış malzeme kalınlığı s0 olsun. (Şekil-2.1: A noktası). Malzeme haddeye girdiği anda ezme kuvveti sıçrama etkisi nedeni ile ∆F kadar artarken, giriş kalınlık değişimi +∆S olacağından çıkış malzeme kalınlığı da ∆s kadar artacaktır. (Şekil-2.1: B noktası).
Çıkış malzeme kalınlığını orijinal set edilen s0 değerine getirebilmek için hadde vidalama veya hidrolik yükleme silindiri ile hadde açıklığını boşta set edilen G0 değerinden G1 değerine kapatmak gerekecektir. Bu durumda ezme kuvveti F’ değerine çıkacaktır. (Şekil-2.1: C noktası).
Şekil-2.1 de görülen A, B, C noktalarının haddedeki görünür fonksiyonları aşağıdaki tabloda işaretlenmiştir.
Şimdi varsayımımızı haddelenecek şerit malzemenin mekanik şekil düzgünsüzlüğünü ve metalürjik yapıdan kaynaklanan iç yapı dinamikleri değişikliklerini göz ardı ederek sabit bir giriş kalınlığı S0 ile yürütelim. (Şekil: 2-2). Haddeleme başlangıcında ezme kuvveti F0 ve boşta hadde açıklığı G0, malzeme giriş kalınlığı S0 ve talep edilen malzeme çıkış kalınlığı s0 olsun.
Malzeme bu konumda haddeye girdiğinde ezme işlemi başlangıcından itibaren malzemenin metalürjik ve mekanik karakteristikleri artma yönünde tepki gösterecek ve haddeleme daha sertleşmiş malzemeye dönüşmüş olacaktır. Bu durumda haddeleme kuvveti ∆F kadar artacak ve çıkış kalınlığı da ∆s kadar artış gösterecektir.
Çıkış kalınlığındaki bu sapmayı düzeltmek için, boşta hadde açıklığını G0 dan G1 değerine düşürmek gerekecektir. Bu durumda yeni haddeleme kuvveti F’ olarak artacaktır.
Hadde yapısında -mill stand housing structure- oluşacak yapı deformasyonu ile hadde sıçraması aşağıdaki şekilde tanımlanır.
Hadde sıçraması = aktif hadde açıklığı – boşta hadde açıklığı = çıkış kalınlığı – boşta hadde açıklığı
Burada, hadde sıçrama eğrisi eğimi non-lineer olup bu yaklaşımda lineere yakın ve sabit alınmıştır. Bu eğim şekil-2.1 de gösterilen ɑ açısının tanjantı ile ilişkilendirilir ve M mill modulus veya elastik modulus olarak adlandırılır ve Gaugemeter / Bisra eşitliği olarak tanımlanır.
Burada F0 / M hesaplanabilen bir veridir. F0 “load-cell” yük hücreleri üzerinden ölçülerek haddeden alınır, M yukarıda ifade edildiği şekilde haddenin devreye alınması aşamasında çıkarılan toplam ezme kuvvetine endekslenmiş hadde sıçrama eğrisi üzerinden endekslenir.
Dolayısı ile hadde çıkışında sabit bir çıkış kalınlığı yakalamak üzere G0 + F0 / M değeri boşta hadde açıklık değeri olarak girilir. Şekil-1.1’deki anlatımda bu değerin sabit kaldığı varsayılmıştır.
Eğer şerit malzeme şekil düzgünsüzlüğü veya malzeme metalürjik iç yapısı nedeni ile F0 değişim gösterdiğinde, buna bağlı olarak G0 da değişim gösterecektir. Bu durumda toplam haddeleme yükü değişim ihtiyacını karşılamak üzere hadde yükleme silindiri ile kontrolü yapılan hadde açıklığı değişimi sürekli olacaktır.
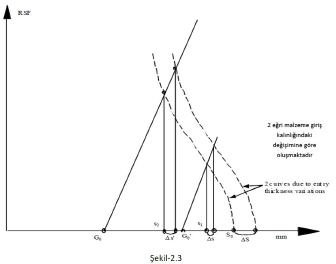
Malzeme kalınlığı (ezme) S0 dan s1 e indiriliyor ise, ∆s kalınlık değişimi olacaktır. Eğer daha büyük bir ezme talebi ile kalınlık S0 dan s2 ye indirilecekse, ∆s’ kalınlık değişimi olur. Ezme miktarı ve dolayısı ile haddeleme kuvveti arttığından ∆s’ kalınlık değişimi, ∆s değişiminden daha büyüktür. Bunun haddelemedeki anlamı ise; haddeleme esnasında kalınlık değişiminin artması o anda hadde merdaneleri altında daha sert ve ezme dayanımı yüksek malzeme bölgesi bulunmasıdır.
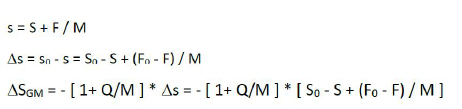
Burada Q malzemeye ait plastic modulus ve M haddeye ait mill modulus dır.
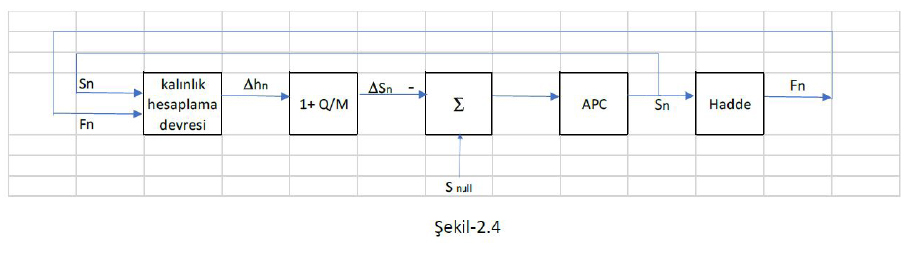
Şerit haddelerinde otomatik kalınlık kontrolü AGC (automatic gauge control) temel yapısı şekil-2.4 de gösterilen kapalı döngü kontrol algoritması şeklinde olup Gaugemeter AGC veya Bisra AGC olarak adlandırılır. Bu gösterimde yer alan APC gösterimi hadde yapısında yer alan hidrolik silindirler, yüksek hız davranışlı servo valfler, hadde açıklığı lineer pozisyon ölçerleri ve kapalı döngü hızlı kontrol algoritmalarını ve kontrol devrelerinin tümünü içerir.
III. Gaugemeter AGC Otomatik Kalınlık Kontrol
Çıkış kalınlık değişimi; mill modulus (M) ve plastik modulus (Q) ile boşta hadde merdane açıklık sapması arasındaki ilişki aşağıdaki şekildedir.
∆h1 = (M / (M - Q)) x ∆s
Çıkış kalınlık sapması ile haddeleme yükü değişimi arasındaki ilişki ise;
∆PR = ∆h1 x Q = {M x Q / (M+Q)} x ∆S şeklinde olup
Burada;
∆h1= Çıkış malzeme kalınlık değişimi (delivery gauge deviation) - mm
∆ho= Giriş malzeme kalınlık değişimi (entry gauge deviation) - mm
∆PR= Haddeleme kuvveti değişimi (rolling load variation) - ton
∆S= Boşta merdane açıklığı değişimi (roll position deviation) - mm
C = Haddelenecek çelik malzeme katsayısı (material constant value)
HCC hidrolik silindir kontrol regülatörü, FSU şerit hadde setup model (finishing mill setup model) algoritması tarafından gönderilen set-up değerlerini referans alarak boşta merdane açıklığını S (roll gap position) hesaplar ve uygular. Bu değer içerisinde hadde sıçraması, mill stand housing deformasyonu, merdane yatak etkileri ve haddelenecek malzemenin plastik deformasyon etkileri göz önüne alınmıştır. Sonuçta şerit haddenin her bir stand ayağında malzeme çıkış kalınlığı;
h1 = S0 + F / M
olarak ifade bulur. Burada M mill modulusun kendisi olup Fooks kanunları ile hesaplanan ∆f = k x ∆X sıçrama modulusunun benzeridir. Bundan dolayı M mill modulus hadde sıçraması (mill stretch veya mill spring curve) olarak adlandırılır. Haddelenen malzemeye uygulanan ezme miktarı ise; ho – h1 = F / M
olarak ifade edilir. M mill modulus ile ezme miktarı arasında lineer olmayan bir doğru orantı mevcuttur.
Başlangıç merdane açıklığı; S = h1 – (Q / M) x (ho – h1) şeklinde olacaktır.
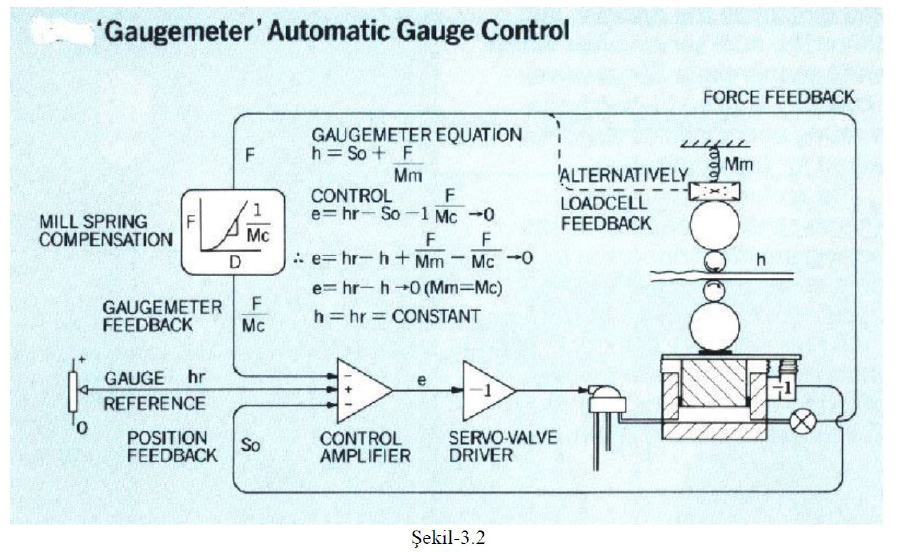
Malzeme haddelenirken ölçülen ezme kuvveti değişimleri PR = PR0 +/- ∆PR başlangıçta set edilen merdane açıklık set değerinde S = S0 - ∆S olarak +/- C x ∆PR / KM ile orantılı değişimler (BISRA AGC output) oluşturacaktır.
HCC hadde açıklığı hidrolik silindirler kontrol regülatörü, hidrolik silindir pozisyonu ve hidrolik akış hareketini sağlayan servo kontrol sistemi, servo valf, basınç geribildirim transdüserleri ve pozisyon transdüserleri birlikteliği bu deplasman değişimini çok hızlı bir şekilde karşılamaktadır.
Haddelemede gerçekçi ve iyi bir hadde açıklık hesaplaması için öncelikle hadde sıçrama – mill modules eğrisinin çok doğru olarak çıkarılması gerekir. Birçok durumlarda lineer bir yaklaşım yeterli olabilir. Ancak, hadde yapısında kompleks ve iç içe birçok mekanik ekipmanlar mevcuttur, ideal durumlar yoktur. Dolayısı ile set edilen hesaplanmış hadde açıklığı ile ve hesaplanmış ezme kuvveti ile yapılan haddelemede kalınlık sapması tam manası ile ortadan kaldırılamayabilir.
BISRA hesaplamalarının doğru ve kararlı yapılması için iyi bir uygulama metodu olarak, hadde boş iken ve merdaneler belirli bir hızda dönme konumunda iken öpüştürülür ve belirlenmiş baskı kuvvetlerine kadar merdaneler kapatılır. Bu metot ile lineer olmayan mill modulus eğrisi çıkartılır. Bu eğri ezme kuvvetine göre hadde sıçrama miktarı hesaplamasında kullanılır.
Genellikle bu ölçme metodu ve hesaplama modelleri bazı düzeltmeler gerektirir. Çünkü bu ölçümler sırasında hadde mekanik yapısı ve merdaneler gerçek haddeleme koşullarındaki çalışma sıcaklıklarına erişmemiştir.
IV. Haddeleme Tesislerinde AGC genel yapısı ve kalınlık düzeltme algoritmaları
Komple bir kalınlık kontrolü (AGC) ve şekil düzgünlüğü (Flatness) için şerit haddelerde aşağıdaki ana tasklar kullanılır.
o Hadde sıçraması düzeltmesi – mill stretch correction, mill spring compensation,
o Gaugemeter AGC düzeltmesi – Gaugemeter AGC lock-ON control,
o İş merdaneleri termal ısınma etkisi – WR thermal expansion compensation,
o Destek merdaneleri yatakları yağ filim kalınlığı değişiminin hadde açıklık etkisi – BUR bearing oil film compensation,
o İş merdaneleri eğme kuvveti ile malzeme profili düzeltme etkisi – WR bending functions gap effects and strip profile corrections,
o İş merdaneleri kaydırma fonksiyonu ile malzeme profili düzeltme etkisi – WR shifting functions,
o Merdane yüzey ısınması ve merdane çap/profil değişimi etkisi – Roll tapering correction,
o Üst destek merdanesi eksantriklik düzeltmesi – BUR roll eccentricity compensation,
o Final çıkış kalınlık ölçme ile kalınlık kontrolü – Monitoring AGC and thickness feedback control,
o İleri adım kontrollü kalınlık düzeltmesi – Feed forward AGC control,
o Malzeme şekil düzgünsüzlüğü kontrolü – Flatness error correction AFC control,
o Öngörülmüş ve düzeltici kalınlık ve profil düzenleme metotları – predictive and adaptive control.
AGC’nin kararlılığı ve doğruluğu, hadde yapısının davranışlarının çok iyi bir şekilde modellenmesine ve ilgili gaugemeter kompanzasyon parametrelerine bağlıdır. Ayrıca mutlak çalışma modu “absolute AGC”nin çalışma modunda tutulması ile kararlılık artırılırken, kontrol sisteminin çevrim davranışının hızı artırılır. Çok ayaklı şerit hadde yapılarında malzeme her bir mill stand ayağına girdikçe mutlak çalışma modu (absolute AGC) aktif olur. Şerit hadde FM set-up modelinin (FSU model) öngörmüş olduğu ezme değerlerine ve her bir standın sıçrama değerlerine göre önceden hesaplanan haddeleme yükleri ve hadde açıklıkları, haddeleme anında ölçülen ezme yükleri ile sonuç kalınlık bilgisi karşılaştırılarak anında hesaplanan düzeltme bilgileri kontrol sistemine uygulanmak üzere gönderilir. Sonuçta hedeflenen şerit çıkış kalınlığı, malzeme boyunca üniform şekil düzgünlüğü yakalanır.
Absolute AGC’nin kararlılığının artırılmasında ikinci adım, “mill deflection” modelinin adaptif geri besleme yöntemi ile bobinden bobine öğrenerek iyileştirilmesi ile mümkündür. Kalınlık kontrolünün kilitlenmesi (lock-on absolute AGC thickness control) metodu ile malzemenin tümü şerit haddede işlenirken hadde çıkışına yerleştirilen X-ray kalınlık ölçme cihazında malzeme boyunca ölçülen kalınlık sapma değerleri bir sonraki malzeme için adaptif hata bilgisi olarak kullanılır.
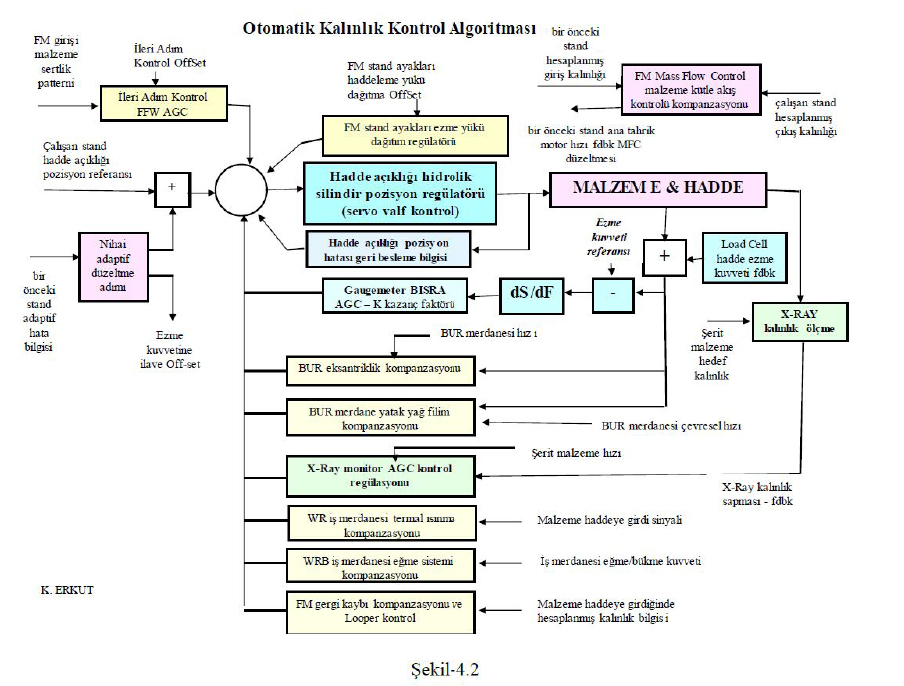
AGC sistemi temel olarak iki ana öğeye ayrılmaktadır. Bunlar Gaugemeter-BISRA AGC ve Monitor AGC dir. Ancak bu kapalı döngü regülasyon adımlarını destekleyen ve alt öğe olarak çalışan kompanzasyon döngüleri de vardır. Bunlar; destek merdaneleri eksantriklik düzeltmesi (BUR eccentricity compensation), merdane yatak yağlama yağ filim yüksekliği düzeltmesi (BUR oil film compensation), iş merdanesi ısıl genleşme düzeltmesi (WR thermal expansion compensation), iş merdanesi eğme sistemi düzeltmesi (WR bending compensation) ve malzeme akışı-gergi kaybı düzeltmesi (material tension loss compensation).
Gaugemeter AGC’nin bir alt kolu olan Absolute AGC, haddeleme standlerinin çıkışında elde edilen malzeme kalınlığını, haddenin önceden belirlenmiş ezme değerlerinde elde edilmiş sıçrama değerlerini (mill modules) kullanarak kontrol sistemi tarafından hesaplanmış hadde açıklığı (roll gap) ve ezme yüküne (rolling force) göre kapalı çevrim regülasyon yaparak kontrol eder. Absolute AGC’nin ana geri besleme elemanı yük hücreleri (load cells) veya alternatif olarak silindir üzerinde bulunan basınç ölçerler (pressure transducers) dir.
Monitor AGC, arzu edilen şerit malzemesi çıkış kalınlığına göre düzeltme yapılarak yüksek hızlı hidrolik silindirler ile hadde açıklığı (gap) haddeleme anında ayarlanmaktadır. Monitör AGC’nin geri besleme elemanı son stand arkasına konulan sabit X-ray kalınlık ölçme cihazıdır. Ayrıca her bir stand üzerinde kurulu merdaneler açıklık ayar hidrolik yükleme silindirlerine mekanik olarak aküple edilmiş ikişer adet yüksek hassasiyetli lineer pozisyon transdüserler mevcuttur. Bu pozisyon ölçerler ile çok hassas ve hızlı olarak hidrolik silindirlerin pozisyonu sürekli ölçülür.
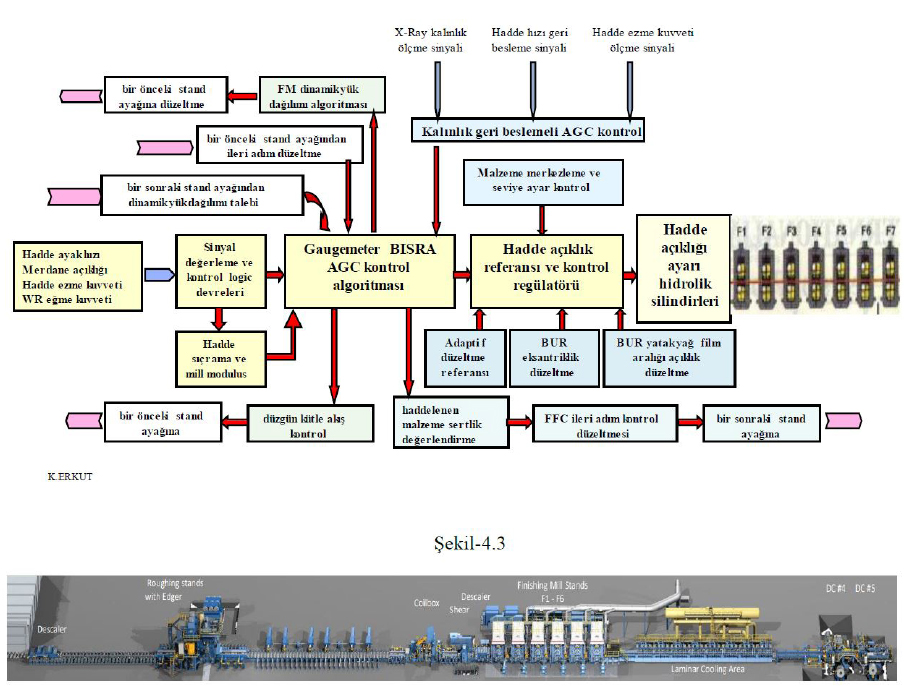
Gaugemeter AGC’nin çalışma prensibi ise; malzeme başının FM son standden çıktığı kalınlık referans alınır ve geride kalan tüm malzeme kalınlığı bu kalınlığa getirilmek üzere regülasyon yapılır. Gaugemeter AGC’nin absolude mode geçirilmesi ile çıkış kalınlığı bilgisayarın set ettiği malzeme nihai çıkış kalınlığı değerine gelecek şekilde kontrol algoritmalarında regülasyon yapılır.
Şekil-4.3 de şerit hadde FM ayaklarında AGC kalınlık kontrol felsefesi ile bununla ilişkilendirilmiş ön ve arka hadde ayaklarındaki malzeme kütle akış kontrol (mass flow control) düzeltmeleri temel yaklaşımı ifade edilmiştir.
KAYNAKLAR:
[1] Fei Zhang, Yongjun Zhang, Jianxin Hou, Ling Huang; Research and Application of Thickness Control Strategies in Steel Plate Rolling, (2014).
[2] Claude Martin; Rolling Theory, The Sendzimir Manual, (2001).
[3] Peter Kucsera, Zsolt Beres; Hot Rolling Mill Hydraulic Gap Control and Thickness Control Improvement, (2015).
[4] A.F. Mac Alister; Modelling and Adaptive Techniques for Rolling Mill Automation - ASIE Year Book, (1989).
[5] Kemal Erkut; Sıcak Haddeleme Tesislerinde Proses Otomasyonu Uygulamaları, 2001 yılı 3-5 Ekim I.Demir-Çelik Sempozyumu.